Karbon nanotüplerin yapısı grafin (
graphene) denilen iki boyutlu balpeteğine benzer karbon tabakalarının yukarıdaki şekilde gösterildiği gibi kıvrılıp bir silindir oluşturması şeklinde tasvir edilebilir. Hesaplamalı fizikte ve kimyada bu yapıların incelenmesi için öncelikle atomlarının koordinatlarının bilinmesi gereklidir. Geçen sene bir konferansda birisi bana bu işi yapabilen bir program bilip bilmediğimi sordu. Ben de hocamdan aldığım onun ABD'deki eski grubundaki birinin yazdığı programı fazla düşünmeden verdim. Ancak sonra böyle bir paylaşımın izinsiz yapılmasının sorun teşkil edebileceği söylendi bana. İnternette ve değişik kimya programlarında bu işi yapan hazır algoritmalar mevcut fakat açık kod olarak bulmak aktif olan bu konudaki rekabetten dolayı olsa gerek pek mümkün değil. Araştırmacılara faydalı olması ümidi ile burada bu iş için python dilinde yazdığım bir programın kodunu ve çalışma mantığını açıklıyorum.

Karbon nanotüpler "kiralite" (chirality) denen (m,n) gibi bir sayı çifti ile tasvir edilirler. Bu (m,n) sayı çifti grafinin baz vektörleri cinsinden kiralite vektörünü tanımlar. Örneğin yukarıdaki şekilde grafinin baz vektörleri a ve b ile gösterilmiş olup (4,2) kiralitesindeki bir nanotüp için kiralite vektörü (C) gösterilmiştir. a vektörünün 4 katı b vektörünün 2 katı ile toplandığı zaman C vektörünü verir.
Peki bu C vektörü ne işe yarar? C vektörü grafin tabakasının nasıl kıvrılıp tüp şekline getirilmesi gerektiğini gösterir. Tabaka öyle kıvrılmalıdır ki vektörün kuyruğundaki ve ucundaki örgü noktaları birbirinin üzerine gelsin. C haricinde önemli olan bir vektör de T vektörüdür. Bu vektör ismini ötelemeden (translation) alır ve tüpün ekseni boyunca kendini tekrarladığı minimum mesafeyi yani hücreyi tanımlar. Elbette ki T vektörü C vektörüne diktir. Nanotübümüzü inşa edebilmek için C'nin yanında T'yi de bilmek gerekir. O zaman işe T'yi hesaplamakla başlayalım. C'ye dik olma koşulunu yazarsak:
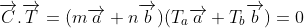
olmak zorundadır. Parantezleri açıp aralarında 60 derece olan a ve b'nin nokta çarpımlarını yaparsak:
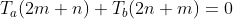
olur ve bu da aşağıdaki şekilde yazılabilir:
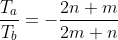
Burada T_a ve T_b'nin en küçük değerleri bize lazımdır. O yüzden sağdaki kesri sadeleştirebildiğimiz kadar sadeleştirmemiz lazımdır. Bunu matematiksel olarak ifade etmek (ve bilgisayara anlatmak) için payın ve paydanın ortak bölenlerinin en büyüğünü (obeb) bulup bölmemiz lazımdır. Böylece T_a ve T_b için aşağıdaki eşitlikleri elde ederiz.
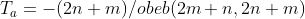

Şimdi buraya kadar olan kısmı bilgisayara anlatmaya çalışalım:
-------------------------------------------------------------
def obeb(A,B):
while A:
A, B = B%A, A
return B
m = input('Lutfen m\'yi giriniz: ')
n = input('Lutfen n\'yi giriniz: ')
hucre = input('Nanotup ekseni boyunca birim hucre sayisi: ')
T_a = -1*hucre*(2*n+m)/obeb(2*m+n,2*n+m)
T_b = hucre*(2*m+n)/obeb(2*m+n,2*n+m)
---------------------------------------------------------------
Elbette en küçük hücreli nanotüpü istemiyor olabiliriz, bu yüzden kullanıcıya kaç birim hücre istediğini de sorduk. En küçük birimi bulmak istiyorsak buraya 1 yazmamız lazım. Obeb için kullandığımız minik ve şirin fonksiyon ise
Öklit algoritması olarak bilinir. T vektörünü hesapladığımıza göre devam edebiliriz. Kıvırma işlemi sonucunda koordinatlarını yazmamız gereken bölge yukarıdaki şekilde gri ile gösterilen C ve T'nin oluşturduğu dikdörtgendir. Bir sonraki aşama bu kısmın içerisinde yer alan örgü noktalarının k ve l indislerinin belirlenmesi olmalıdır. Mesela şekildeki K noktası (1,3) indislerine sahiptir (1a+3b). İşte meselemiz hangi indis çiftinin gri bölge içerisinde yer alacağıdır. Bunu yapmak için vektörel çarpıma başvuruyoruz. Seçilen herhangi bir K noktasının içeride kalması için aşağıdaki eşitsizliklerin hepsinin sağlanması gerekmektedir:
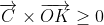
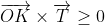
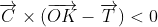
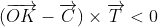
Böyle birşey yazdığım için matematikçiler bana kızabilirler zira vektörlerle sayılar kıyaslanamaz ama burada kastettiğim şey sonuç vektörünün sayfanın dışına doğru mu içine doğru mu baktığıdır. Yani z-koordinatlarının işaretleridir. Parantezleri açıp vektörel çarpımları yaptığımızda bu ifadeyi aşağıdaki iki eşitsizlik haline getirebiliriz:
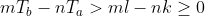
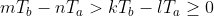
Şimdi bu söylediklerimizi koda dökme zamanı. Aklımda olan şey k'ya ve l'ye belli aralıktaki değerler için döngü yaptırıp yukarıdaki koşulu sağlayan çiftleri bir listeye kaydetmek. Tabii aralık ne olacak sorusu var; bunun için m,n,T_a ve T_b indislerinin toplamı yeterli olması lazım.
-----------------------------------------------------
aralik = m + n + abs(T_a) + abs(T_b) + 2
kl_listesi = [ ]
for k in range(-aralik,aralik):
for l in range(-aralik,aralik):
if (m*l-n*k) >= 0 and (m*T_b-n*T_a) > (m*l-n*k):
if (k*T_b-T_a*l) >= 0 and (m*T_b-n*T_a) > (k*T_b-T_a*l):
kl = [ ]
kl.append(k)
kl.append(l)
kl_listesi.append(kl)
------------------------------------------------------
Böylece kl_listesi'ni ihtiyacımız olan ikililerle doldurmuş oluruz. Şimdi artık atomları yerleştirmeye (koordinatlarını yazmaya) başlayabiliriz. Bunun için elbette birim hücrede yer alan atomları önceden bir listeye yazmak gerek. Grafin'in birim hücresinde iki karbon atomu bulunur. Bunlar şekildeki içi dolu ve boş noktalarla gösterilmiştir. Yine içiçe döngü ile her baz atomunu kl_listesindeki her ikili ile eşleştirip ötelemek lazımdır. Tabii bir de baz vektörlerini de artık yazmanın vakti geldi. Bunu da grafindeki karbon-karbon bağı uzunluğu olan 1.42 Angstrom cinsinden yazabiliriz.
-------------------------------------------------------
bag_uzunlugu = 1.42
a_x = bag_uzunlugu*(3**0.5)
a_y = 0.0
b_x = a_x/2
b_y = b_x*(3**0.5)
baz_atomlari = [[0,0],[b_x,bag_uzunlugu/2]]
atom_listesi = [ ]
for i in kl_listesi:
for j in baz_atomlari:
koordinatlar = [ ]
koordinatlar.append(j[0]+i[0]*a_x+i[1]*b_x)
koordinatlar.append(j[1]+i[0]*a_y+i[1]*b_y)
atom_listesi.append(koordinatlar)
-----------------------------------------------------
Artık gri dikdörtgendeki atomların x-y koordinatları atom_listesi'nin içinde. Şimdi bu dikdörtgeni kıvırıp bir nanotüp yapmak istiyoruz. Bu işi yapan programlar genelde nanotüp eksenini z-ekseni ile çakışık hale getirirler. Bunu yapmanın en kolay yolu x-y eksenine göre teta açısı kadar yan duran dikdörtgenimizi "düzeltmek"ten geçer. Düzeltme ile kast ettiğimiz şey bir koordinat dönüşümüdür. Bir koordinat sistemini orjini etrafında saat yönünün tersinde teta açısı kadar döndürdüğünüzde yeni koordinatlar aşağıdaki formülle verilir.
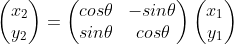
Biz koordinat sistemimizi saat yönünde döndürmek istiyoruz dolayısı ile teta'nın işareti negatiftir bu da sadece sinüslerin işaretini ters çevirir. Elbette ki önce teta açısını hesaplamamız gerekir, bunun için de C vektörünün bileşenlerine ihtiyacımız vardır. Bir de trigonometrik fonksiyonları kullanma için python'un math modülünü çağırmamız gerekmektedir.
--------------------------------------------------
C_x = a_x*m + b_x*n
C_y = a_y*m + b_y*n
C_boy = (C_x**2 + C_y**2)**0.5
import math
teta = math.acos(C_x/C_boy)
dondurulmus = [ ]
for i in atom_listesi:
koordinatlar = [ ]
koordinatlar.append(i[0]*math.cos(teta)+i[1]*math.sin(teta))
koordinatlar.append(-1*i[0]*math.sin(teta)+i[1]*math.cos(teta))
dondurulmus.append(koordinatlar)
---------------------------------------------------
Artık dikdörtgenimizin içinde yer alan atomlar yukarıdaki şekildeki gibi kayıt edilmişlerdir. (Dikey eksen henüz halen y-eksenidir ama bir sonraki basamakta y koordinatını z-koordinatı olarak yazacağız, burada yandaki şekille karışmasın diye erkenden z olarak isimlendirdik.) Son basamak olan kıvırma işlemini yapabilmek için bütün atomları yanda gösterildiği gibi bir çemberin üzerine dizmek gereklidir. C vektörünün uzunluğu çemberin çevresidir ve A'nın x koordinatının C'nin boyuna oranının 2 pi ile çarpımı alfa açısını radyan cinsinden bize verir. x ve y koordinatları alfanın trigonometrik oranları cinsinden yazılabilir:
------------------------------------------------------
T_x = a_x*T_a + b_x*T_b
T_y = a_y*T_a + b_y*T_b
T_boy = (T_x**2 + T_y**2)**0.5
R = C_boy/(2*math.pi)
kivrilmis = [ ]
for i in dondurulmus:
koordinatlar = [ ]
alfa = 2*math.pi*i[0]/C_boy
koordinatlar.append(R*math.cos(alfa))
koordinatlar.append(R*math.sin(alfa))
koordinatlar.append(i[1]-T_boy/2) # orjini z boyunca ortalamak icin
kivrilmis.append(koordinatlar)
---------------------------------------------------------
Artık sadece yazdırmak kaldı. Bunu birçok kimya programının tanıdığı standart .xyz dosyası formatında yapalım. Bu formatta önce başa toplam atom sayısı yazılır, sonraki satır açıklamalara ayrılmıştır (boş bırakılabilir) ve sırasıyla atom sembolü, x,y ve z koordinatları araya boşluk bırakarak yazılır.
---------------------------------------------------------
print len(kivrilmis)
print
for i in kivrilmis:
print '%s %8f %8f %8f' % ('C',i[0],i[1],i[2])
----------------------------------------------------------
Çıktıyı bir dosyaya yazdırıp MOLEKEL programı ile çizdirdiğim 4 birim hücreli bir (5,5) nanotüpün resmi aşağıdadır.

Evet! Bu kısa kodla ilk resimde gösterilen işlemi yapmış olduk. Aynı mantıkla çalışan bir kodla prensipte sadece grafinden yuvarlanarak yapılan nanotüpler değil her türlü peryodik düzlemsel yapıdan elde edilebilecek nanotüplerin koordinatlarını bulmak mümkündür. Aynı "kiralite" mantığı birçok farklı yapıya genelleştirilip kullanılabilir.
Yapılması gereken değişiklik baz vektörlerinde ve baz atomlarındadır. Bir de T vektörünü indisler cinsinden bulurken kodu yazmadan önce matematiği yukarıda gösterdiğimiz metod ile elle yapmak ve tam sayılar cinsinden bir formül türetmeye çalışıp ondan sonra koda yazılmalıdır zira bu işi baz vektörleri bileşenlerinden bilgisayarlara yaptırmaya kalkmak "floating point" meseleleri yüzünden riskli ve zahmetlidir. Yine gerekli indisleri yazdırırken kullanılan vektörel çarpımlar yeni baz vektörlerine göre kontrol edilmelidir. En kritik hususlar bunlardır.
Bunlar haricinde nanotüpü eksen boyunca germe, sıkıştırma, eksene dik ölçeklendirme (şişirme veya büzüştürme) veya eksen etrafında burma küçük modifikasyonlarla elde edilebilir. Bu modifikasyonların da eklendiği en genel programı aşağıda veriyorum. ### ile işaretli yerler grafin dışında bir yapı ile çalışılmak isteniyorsa değiştirilmesi gereken yerlerdir. Son olarak seçtiğiniz baz vektörlerinin axb vektörel çarpımının pozitif olması lazımdır.
-----------------------------------------------------------------
import math # Trigononetrik fonksiyonlar icin lazim
def obeb(A,B): # Ortak bolenlerin en buyugu fonksiyonu
while A:
A, B = B%A, A
return B
### bag_uzunlugu = 1.42
### a_x = bag_uzunlugu*(3**0.5)
### a_y = 0.0
### b_x = a_x/2
### b_y = b_x*(3**0.5)
### baz_atomlari = [['C',0,0],['C',b_x,bag_uzunlugu/2]]
print 'Kiralite (m,n) olarak tanimlaniyor'
m = input('m\'yi giriniz: ')
n = input('n\'yi giriniz: ')
hucre = input('Hucre sayisini giriniz: ')
T_olcek = input('T olceklendirmesi: ')
C_olcek = input('C olceklendirmesi: ')
burulma = input('Burulma acisi (derece): ')
### T_a = -1*hucre*(2*n+m)/obeb(2*m+n,2*n+m)
### T_b = hucre*(2*m+n)/obeb(2*m+n,2*n+m)
aralik = m + n + abs(T_a) + abs(T_b) + 2
kl_listesi = [ ]
for k in range(-aralik,aralik):
for l in range(-aralik,aralik):
if (m*l-n*k) >= 0 and (m*T_b-n*T_a) > (m*l-n*k):
if (k*T_b-T_a*l) >= 0 and (m*T_b-n*T_a) > (k*T_b-T_a*l):
kl = [ ]
kl.append(k)
kl.append(l)
kl_listesi.append(kl)
atom_listesi = [ ]
for i in kl_listesi:
for j in baz_atomlari:
koordinatlar = [ ]
koordinatlar.append(j[0])
koordinatlar.append(j[1]+i[0]*a_x+i[1]*b_x)
koordinatlar.append(j[2]+i[0]*a_y+i[1]*b_y)
atom_listesi.append(koordinatlar)
C_x = a_x*m + b_x*n
C_y = a_y*m + b_y*n
C_boy = ((C_x**2 + C_y**2)**0.5)
teta = math.acos(C_x/C_boy)
dondurulmus = [ ]
for i in atom_listesi:
koordinatlar = [ ]
koordinatlar.append(i[0])
koordinatlar.append(i[1]*math.cos(teta)+i[2]*math.sin(teta))
koordinatlar.append(-1*i[1]*math.sin(teta)+i[2]*math.cos(teta))
dondurulmus.append(koordinatlar)
T_x = a_x*T_a + b_x*T_b
T_y = a_y*T_a + b_y*T_b
T_boy = T_olcek*((T_x**2 + T_y**2)**0.5)
R = C_olcek*C_boy/(2*math.pi)
kivrilmis = [ ]
for i in dondurulmus:
koordinatlar = [ ]
alfa = 2*math.pi*i[1]/C_boy
beta = (T_olcek*i[2]*burulma/T_boy)*(math.pi/180)
koordinatlar.append(i[0])
koordinatlar.append(R*math.cos(alfa+beta))
koordinatlar.append(R*math.sin(alfa+beta))
koordinatlar.append(T_olcek*i[2]-T_boy/2)
kivrilmis.append(koordinatlar)
cikti = [ ]
for i in kivrilmis:
a = '%s %8f %8f %8f\n' % (i[0],i[1],i[2],i[3])
cikti.append(a)
isim = raw_input('Lutfen cikti dosyasi icin bir isim giriniz: ')
dosya = file(isim,'w')
dosya.write(str(len(atom_listesi)))
dosya.write('\n')
a = '('+str(m)+','+str(n)+') Nanotup. R = '+str(R)+' Ang. T = '+str(T_boy)+' Ang.\n'
dosya.write(a)
for i in cikti:
dosya.write(i)
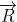 vektörü ile; dünya üzerinde
vektörü ile; dünya üzerinde  paraleli ve
paraleli ve 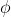 meridyeninde bulunan gözlemcinin konumunu ise
meridyeninde bulunan gözlemcinin konumunu ise 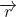 vektörü ile gösterelim. Bu durumda uyduya bakan gözlemci
vektörü ile gösterelim. Bu durumda uyduya bakan gözlemci 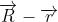 vektörü yönünde bakmaktadır.
vektörü yönünde bakmaktadır.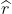 vektörü gök kubbenin "doruğunu" (zenith) gösterirken
vektörü gök kubbenin "doruğunu" (zenith) gösterirken 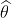 vektörü coğrafi kuzeyi (manyetik kuzeyle karışmasın)
vektörü coğrafi kuzeyi (manyetik kuzeyle karışmasın) 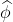 vektörü ise coğrafi doğu istikametini göstermektedir. Şapka sembolü birim vektörleri ifade etmektedir.
vektörü ise coğrafi doğu istikametini göstermektedir. Şapka sembolü birim vektörleri ifade etmektedir.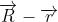 vektörünün küresel sistemdeki birim vektörler yönünde izdüşümlerini bulmakdır. Böylece hangi coğrafi yönde ve ufuktan kaç derece yukarı bakılması gerektiğini bulmuş oluruz.
vektörünün küresel sistemdeki birim vektörler yönünde izdüşümlerini bulmakdır. Böylece hangi coğrafi yönde ve ufuktan kaç derece yukarı bakılması gerektiğini bulmuş oluruz.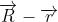 vektörünün
vektörünün 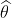 (kuzey) ile
(kuzey) ile  (doğu) üzerinde izdüşümlerinin oranını hesaplayacağız. Bu oran bize yönü bildiren
(doğu) üzerinde izdüşümlerinin oranını hesaplayacağız. Bu oran bize yönü bildiren 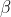 açısının tanjantını verecektir.
açısının tanjantını verecektir.














