Güneş Saati (Hobi Projesi)

Oldum olası güneş saatlerine bir hayranlığım ve hatta “zaafım” var. Konu üzerinde ne zaman düşünsem kendimi detaylara yoğunlaşmış buluyorum. Gölgelerin hareketinin analitik ifadesinde insanı büyüleyen birşey var. Bir süredir aklımdaydı bir güneş saati yapmak. Yapmak derken internetten bulabileceğiniz hazır şablonlardan birini kullanmayı kastetmiyorum. Hesabını, kitabını yapıp çizgilerini çizmeye kadar her aşamasını kendim yapabilirim diye düşünüyordum. Böyle bir işlem için gerekli olan şeyler:

A)   Temel Astronomi ve Coğrafya Bilgisi

Enlem kavramı, kutup yıldızı, gök cisimlerinin gün içindeki hareketi, güneşin deklinasyonu gibi konularda bilgi sahibi olmak.

B)   Analitik Geometri Bilgisi

Konik kesitler, koninin yüzey denklemi, düzlem denklemi, kartezyen koordinat sistemleri, koordinat sistemi öteleme dönüşümü, koordinat sistemi döndürme dönüşümü, kesiştirme gibi kavramlara hakim olmak gerekmekte.

Bunun haricinde sadece denklemleri hesaplamayacağım aynı zamanda eğrileri çizmek ve güneş saatini de yapmak istiyorum derseniz:

C)    Kodlama Bilgisi

Bir grafik çizme programına hakim olmak gerekiyor. Ben GNUPLOT kullandım, bir de görsellerin üzerinde oynamak için bir program kullanmak gerekiyor. Her pratik işte olduğu gibi MS Powerpoint işimi fazlasıyla gördü.

D)   Diğer şeyler

Son olarak çizgilere tarih etiketi yazabilmek için güneşin deklinasyon tablosu, ve saatleri global saat cinsinden düzeltmek için zaman düzeltme (equation of time) grafiği bilgileri de lazım olacak. İnternetten kolayca bulunabilecek bir deklinasyon tablosu ve düzeltme grafiği işimi gördü.

Geçen pazar günü havanın da güneşli olmasının getirdiği motivasyonla hesap kitap işine giriştim. Çetrefilli olan kısım gölgenin gün içerisindeki hareketinin çizdiği eğriyi hesaplamak. Bu eğri bizim enlemlerde bir hiperbole karşılık geliyor. Sebebini anlamak için gök cisimlerinin hareketini ve konik kesitleri anlamamız lazım.

Dünya kendi ekseni etrafında dönerken dünyadan gökyüzüne bakan biri bütün gök cisimlerini sanki kutup yıldızının etrafında dönüyormuş olarak görür. Yukarıdaki fotoğraf bu olguyu çok iyi ifade etmektedir. Bulutsuz bir yaz gecesi birkaç saatlik uzun bir pozlama süresi ile çekilen bu fotoğrafta tüm yıldızların belli bir nokta etrafında döndükleri açıkca gözükmektedir. Merkezdeki yıldız kutup yıldızı ismi ile bilinmekte olup dünya eksen doğrultusunun üzerinde yer aldığı için bu hareketten hemen hemen hiç etkilenmez ve daima aynı yerde durur. (Gündüz de oradadır ama elbette atmosfer ışımasından onu göremeyiz.)

İşte güneş de bir gün içerisinde böyle bir çember üzerinde gezmektedir. Bu süre zarfında ondan bize gelen ışığın taradığı yüzey de elbette ki bir koninin yan yüzeyini oluşturur. Aşağıdaki şekil tam kuzey kutbundan bakan bir gözlemcinin güneşi ve güneş altındaki bir cismin gölgesinin hareketini göstermektedir.

Bu özel durumda cismin gölgesi bir çember çizmektedir çünkü gözlemcinin düşey ekseni ile dünyanın ekseni aynıdır ve gözlemcinin üzerinde durduğu yatay düzlem ışık konisini dik bir şekilde kesmektedir. Farklı enlemlerde ise durum böyle değildir, dünyanın ekseni ile gözlemcinin düşeyi çakışmaz ve koniyi biraz açılı çizmek gerekir. Aşağıdaki şekil tipik bir durumu göstermektedir.

Görüldüğü gibi gözlemcinin düzlemi ışık konisini belli bir açı ile kesmektedir. Bu durumda ortaya çıkacak eğrinin ne olacağını bulmak istiyoruz. Bu eğriler genel olarak konik kesitler olarak isimlendirilirler ve düzlemin koniyi hangi açıyla kestiğine bağlılık gösterirler.

İlk örneğimize dönecek olursak kutuptan güneye doğru gittiğimizde koni de giderek daha yatay hale gelir ve gölgelerin çizdiği eğriler sırası ile elipse, ondan sonra parabole ve en sonunda da hiperbole dönerler. Bizim ülkemizin enlemlerinde bu eğriler daima hiperbol şeklinde görülürler. (Parabol veya elips görmek için yazın güneşin hiç batmadığı kuzey enlemlerine kadar çıkmak gerekir; diğer her yerde gölgeler hiperbol çizer.)

Peki bu hiperbolü güneş saatimizin yüzüne çizmek istiyoruz o yüzden de denklemini hesaplamaya ihtiyacımız var. Bu denklemi hesaplamak için üç tane büyüklüğü bilmemiz gerekmektedir. Bunlardan birincisi elbette ki coğrafi konumumuzun enlemidir. Bunu 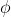 sembolü ile göstereceğiz. Bir diğer büyüklük güneş saatimizde gölge yaratacak cismin yerden yüksekliğidir. Buna da h diyeceğiz. Son olarak koninin tepe açısına etkisi olacağından dolayı düneşin deklinasyonunu bilmemiz gerekecektir.  Deklinasyon ile kastedilen şey güneşin dünyanın ekvator düzleminden açısal uzaklığıdır ve bu değer  yıl içerisinde +23,5 ve -23,5 derece arasında değişir. Güneşin deklinasyonunu da  ile gösterelim.

İlk başta koninin denklemini yazmak gerekecektir. Bu işi koninin tepe noktasını orijin kabul eden ve bir ekseni koninin simetri ekseni ile çakışık bir koordinat sisteminde yapmak en kolayıdır. Aşağıdaki şekilde böyle bir koordinat sisteminin eksenleri  olarak gösterilmiştir.

 ile gösterilen koordiat sistemi ise güneş saatimizin koordinat sistemini ifade etmektedir. Bu koordinat sisteminin orjini gölge yapacak cismin tam altında yer almaktadır ve x ekseni kuzeyi y ekseni de batıyı göstermektedir. Ancak bu koordinat sisteminde koninin denklemini yazmak kolay değildir. O yüzden koni için en “doğal” koordinat sistemi olan  koordinat sistemindeki noktaları  değerlerine nasıl dönüştürebileceğimizi bulmamız lazımdır. Bunu iki aşamada yapabiliriz. Önce  koordinat sistemini  yönünde  kadar öteleyip  koordinat sistemine geçeriz. Ondan sonra da bu koordinat sistemini  ekseni etrafında  derece kadar döndürürüz. Bu dönüşümler aşağıdaki gibi yazılabilir.

      (1)

Birbirini 90 dereceye tamamlayan açıların trigonometrik özelliklerini kullanıp matris (1) denklemni 3 ayrı denklem şeklinde yazarsak:

        (2)
                                          (3)
        (4)

Ayrıca öteleme dönüşümünden 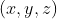 ile 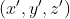 arasındaki bağıntı aşağıdaki şekilde yazılabilir.

               (5)
               (6)
       (7)

(2), (3), (4) ve (5), (6), (7) de verilen dönüşümler birleştirilirse 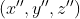 den 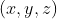 ye geçebiliriz:

           (8)
                                                        (9)
            (10)

Şimdi 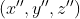 sisteminde koninin denklemini basitçe yazalım:

               (11)

Burada  güneşin deklinasyonunu ifade etmektedir. Şimdi elde ettiğimiz (8), (9), (10) numaralı dönüşümleri (11) nolu denklemde yerine yazarak koninin denklemini 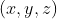 koordinatları cinsinden yazabiliriz. Ayrıca bu koni ile kesiştireceğimiz düzlemin denklemi 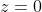 olduğundan bu denklemde  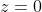yazarak istediğimiz düzlem ara kesitini de pratik bir biçimde bulmuş oluruz. İşlemden tasarruf etmek için bu iki adımı aynı anda yapalım:

       (12)

Bu ifade düzenlendiği zaman aradığımız denklem elde edilir:

              (13)

(13) nolu denklem yerden 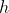 kadar yukarıda bulunan noktasal bir cismin gölgesinin takip edeceği eğrilerin genel denklemidir. Eğrilerin dememizin sebebi yılın farklı zamanlarında güneşin deklinasyonu değişeceğinden dolayı farklı  değerleri için farklı eğriler söz konusudur. Burada ilginç olan bir durum ’nın denklemde bulunduğu her yerde sinüsünün karesi alınmaktadır. Yani pozitif ve negatif deklinasyon değerleri aynı eğrileri verir. İlk başta şaşırtıcı gelebilecek bu durum esasında normaldir. Çünkü hiperbol eğrisi her zaman çiftler halinde ortaya çıkar. Bunlardan birisi pozitif deklinasyona karşılık gelen tarihteki çizgiye diğeri ise negatif deklinasyon durumuna karşılık gelir.

(13) nolu denkleme bakıldığında görülebilecek bir diğer hususiyet ise ’nın sıfır olması durumunda denklemde tanımsız terimlerin olmasıdır. Böyle bir durumda zaten artık bir koniden bahsedilemez ve güneş ekvator ile aynı düzlemdedir. 21 Mart ve 21 Eylül’de gerçekleşen ve ekinoks denen bu durumda gölgeler bütün dünyada düz bir doğru üzerinde ilerlerler.

Hiperbol eğrileri güneş saatimize baktığımızda tarihi bulmamızı sağlar ancak saati nasıl anlayacağız sorusuna henüz değinmedik. Yine koninin doğal koordinat sistemi olan  sistemine dönecek olursak  ve  bir çember üzerinde yer aldıkları için aşağıdaki gibi zamanın fonksiyonu olarak ifade edilebilirler:

                (14)

                 (15)

Burada 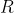 rastgele bir çemberin yarıçapını göstermekte olup birazdan göstereceğimiz metoddan ötürü bir anlamı ve önemi yoktur.  ise saat cinsinden tam yerel öğle vaktinden itibaren zamanı ifade eder. Güneş bir turunu 24 saatte tamamladığından dolayı bir saatte 15 derece kadar dönmektedir; denklemdeki 15 buradan gelir. Şimdi daha önce bulduğumuz (8), (9), (10) dönüşümlerini kullanarak (14) ve (15) nolu denklemleri 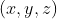  koordinat sistemine göre aşağıdaki gibi yazabiliriz. 

       (16)

                                                    (17)

 düzleminde olduğumuzdan yine  yerine sıfır koyup iki denklemi birbirine bölersek ’ler sadeleşir ve aşağıdaki ifadeyi bulmuş oluruz.

              (18)

Bu ise aşağıdaki şekilde yazıldığında görüleceği gibi bir doğru denkleminden başka bir şey değildir:

       (19)

Farklı saatlerde  değiştiği için gölgeler farklı doğrular üzerinde yer alacaklardır. Öyle ise güneş saatimizde saati de ölçmek istiyorsak hiperboller haricinde bu doğruları da çizmemiz gerekir.

Ben bu çizim işlemlerini gerçekleştirmek için GNUPLOT isimli bir program kullandım. Bu programda denklemleri istediğiniz gibi yazıp eğrilerinizi çizebiliyorsunuz. Kullandığım betiki (scripti) yazının en sonunda bulabilirsiniz.

Sonuç olarak İstanbul için (yani 41 derece kuzey enlemi için) 15 farklı deklinasyon değerine karşılık gelen hiperbolleri (denklem (13)) ve 15 farklı saat değerine karşılık gelen doğruları (denklem (19)) olan bir güneş saati yüzü çizdim. Çizimden sonra da oluşturduğum görseli powerpoint’e kopyaladım ve bir deklinasyon tablosuna bakarak üzerine tarihleri ekledim. Ayrıca bir de zaman düzeltme grafiği ekledim. Sonuç olarak aşağıdaki şey ortaya çıktı.

(Resmin üzerine tıklayınca orjinal boyutunda görebilirsiniz, indirip çıktısını alabilirsiniz.)

Tarih çizgileri ve saat doğruları hemen gözümüze çarpan özellikler. Belki ilk olarak göze çarpan şey saat doğrularının bir noktada birleşiyor olması. O noktayı koordinat sistemimizin orjini zannedebilirsiniz ama öyle değil. Burada koordinat sisteminin orjini o noktanın biraz sağında yer alan küçük işaretli noktadır. Bu güneş saatini kullanmak için en sağdaki üçgeni kesmeniz ve doğruların kesiştiği nokta ile işaretli nokta arasına dik olarak yerleştirmeniz gereklidir. (Koordinat sisteminin 1 birimi üçgenin yüksekliği kadardır.) Üçgeni dik tutabilmek için iki tane tavla zarının arasına yapıştırdım. (Siz daha yaratıcı yöntemler bulabilirsiniz.)

Zaman ve tarih okurken dikkat edilecek husus gölgenin EN UCUNUN düştüğü hiperbol çizgisinden tarihi, üçgenin HİPOTENÜSÜNÜN gölgesinin DOĞRULTUSUNDAN da saati okumanız gerekliliğidir. (Üçgenin dikey kenarının gölgesinin yönünün bir anlamı yoktur. Bu kafa karıştırıcı olabilir.)

Saati kullanma talimatları şöyledir:

1.  Görselin istediğiniz boyutta bir çıktısını alın. (A3 tavsiye ederim.)

2. Üçgeni dikkatlice kesip çıkarın. (Üçgenin boyutları önemlidir, tam çizgilerinden kesmek gereklidir.)

3. Saati güneş alan bir yere yerleştirin. Zeminin tam yatay olması önemlidir.

4. Üçgeni doğruların kesiştiği nokta ile onun biraz ilerisinde işaretli nokta arasına tam dik bir şekilde yerleştirin. (Dik durması için tavla zarı gibi iki küçük cisim arasına yapıştırılabilir.)

5. Şimdi üçgenin konumunu bozmadan saatin simetri eksenini kuzeye döndürmemiz gerekmektedir. Eğer kuzeyi bilmiyorsanız ama tarihi biliyorsanız bu çok kolay bir şekilde yapılabilir. Üçgenin tam tepe noktasının gölgesi uygun tarih eğrisinin üzerine düşene kadar saat bütünüyle döndürülür. (Benzer bir mantıkla bu saati kullanarak sadece saati biliyorsanız kuzeyi ve tarihi, sadece kuzeyi biliyorsanız tarihi ve saati bulabilirsiniz.)

6. Saat kuzeye döndürüldüğünde hipotenüsün gölgesinin doğrultusu size saati gösterir. Yeşil çizgilerle karşılaştırarak öğle zamanından kaç saat geride veya ileride olduğunuzu bulabilirsiniz. (Eğer yaz saatinde değilseniz öğlen saat 12:00 eğer yaz saatindeyseniz öğlen saat 13:00 civarındadır.) Yeşil çizgilerin her biri bir saate karşılık gelir.

7. Üçgenin tepe noktasının gölgesinin gün boyu üzerinde gezdiği eğri tarih bilgisine karşılık gelir. (Aynı eğriye karşılık gelen iki farklı tarih olduğuna dikkat ediniz. Deklinasyonun azaldığı tarihler saatin bir tarafına arttığı tarihler diğer tarafına işlenmiştir.)

8. Saatin üzerinde gördüğünüz grafik yıl içerisinde güneş saatinin ne kadar ileri veya geri kalacağını gösterir. Örnek olarak Mayıs ayının ortasında güneş saatiniz tam öğle vaktini gösterdiğinde grafik -3 civarını göstermektedir yani gerçek saat 12:03 anlamına gelir. Bu düzeltmenin sebebi dünyanın ekseninin eğikliği ve dünyanın güneş etrafında eliptik bir yörüngede dönmesidir.

8. maddede bahsedilen grafik “Equation of time” ismiyle bilinir ve güneş saatlerinde yaygın olarak kullanılır.

Eğrileri çizmek için kullandığım gnuplot scripti aşağıdadır:

set term postscript eps enhanced color font "Helvetica" 24
set output 'face.eps'
set nokey
#set grid  # kontrol amacli
unset border
set xrange[-3:3]
set noxtics
set noytics
set yrange[-4:4]
set samples 1000000
lat = 41*pi/180
h = 1
set parametric
set trange [0:1]
p(t)= A + t*(B-A)
set arrow from  -h/tan(lat),0 to 2,0 nohead lt 2  # Kuzey guney hatti
set arrow from -h/tan(lat),-3.6 to -h/tan(lat),3.6 nohead lt 2
set arrow from 0,-0.05 to 0,0.05 nohead lt 2     # Orijin isareti
set arrow from tan(lat),-4 to tan(lat),4 nohead lt 2     # Ekinoks cizgisi
set arrow from 2.1,0 to 2.1+(1/tan(lat)),0 nohead lt 2     # Ucgenin alt kenari
set arrow from 2.1+(1/tan(lat)),0 to 2.1+(1/tan(lat)),1 nohead lt 2  #Ucgenin dik kenari
set arrow from 2.1+(1/tan(lat)),1 to 2.1,0 nohead lt 2     # Ucgenin hipotenusu
set size ratio -1
plot A = -8, B = 8, p(t), ((cos(lat)**2/sin(-23.04*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(-23.04*pi/180)**2)*p(t) + (sin(lat)**2/sin(-23.04*pi/180)**2 -1*h**2))**0.5 w l lt 1,\
A = -8, B = 8, p(t), -((cos(lat)**2/sin(-23.04*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(-23.04*pi/180)**2)*p(t) + (sin(lat)**2/sin(-23.04*pi/180)**2 -1*h**2))**0.5 w l lt 1,\
A = -8, B = 8, p(t), ((cos(lat)**2/sin(-20.05*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(-20.05*pi/180)**2)*p(t) + (sin(lat)**2/sin(-20.05*pi/180)**2 -1*h**2))**0.5 w l lt 6,\
A = -8, B = 8, p(t), -((cos(lat)**2/sin(-20.05*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(-20.05*pi/180)**2)*p(t) + (sin(lat)**2/sin(-20.05*pi/180)**2 -1*h**2))**0.5 w l lt 6,\
A = -8, B = 8, p(t), ((cos(lat)**2/sin(-17.2*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(-17.2*pi/180)**2)*p(t) + (sin(lat)**2/sin(-17.2*pi/180)**2 -1*h**2))**0.5 w l lt 2,\
A = -8, B = 8, p(t), -((cos(lat)**2/sin(-17.2*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(-17.2*pi/180)**2)*p(t) + (sin(lat)**2/sin(-17.2*pi/180)**2 -1*h**2))**0.5 w l lt 2,\
A = -8, B = 8, p(t), ((cos(lat)**2/sin(-12.16*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(-12.16*pi/180)**2)*p(t) + (sin(lat)**2/sin(-12.16*pi/180)**2 -1*h**2))**0.5 w l lt 7,\
A = -8, B = 8, p(t), -((cos(lat)**2/sin(-12.16*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(-12.16*pi/180)**2)*p(t) + (sin(lat)**2/sin(-12.16*pi/180)**2 -1*h**2))**0.5 w l lt 7,\
A = -8, B = 8, p(t), ((cos(lat)**2/sin(-7.5*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(-7.5*pi/180)**2)*p(t) + (sin(lat)**2/sin(-7.5*pi/180)**2 -1*h**2))**0.5 w l lt 3,\
A = -8, B = 8, p(t), -((cos(lat)**2/sin(-7.5*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(-7.5*pi/180)**2)*p(t) + (sin(lat)**2/sin(-7.5*pi/180)**2 -1*h**2))**0.5 w l lt 3,\
A = -8, B = 8, p(t), ((cos(lat)**2/sin(4.18*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(4.18*pi/180)**2)*p(t) + (sin(lat)**2/sin(4.18*pi/180)**2 -1*h**2))**0.5 w l lt 4,\
A = -8, B = 8, p(t), -((cos(lat)**2/sin(4.18*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(4.18*pi/180)**2)*p(t) + (sin(lat)**2/sin(4.18*pi/180)**2 -1*h**2))**0.5 w l lt 4,\
A = -8, B = 8, p(t), ((cos(lat)**2/sin(14.54*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(14.54*pi/180)**2)*p(t) + (sin(lat)**2/sin(14.54*pi/180)**2 -1*h**2))**0.5 w l lt 5,\
A = -8, B = 8, p(t), -((cos(lat)**2/sin(14.54*pi/180)**2 -1)*p(t)**2 -(h*sin(2*lat)/sin(14.54*pi/180)**2)*p(t) + (sin(lat)**2/sin(14.54*pi/180)**2 -1*h**2))**0.5 w l lt 5,\
A = -h/tan(lat), B = 0.3, p(t), tan(15*pi/180)*(sin(lat)*p(t) + h*cos(lat)) lt 2, A = -h/tan(lat), B = 0.3, p(t), -tan(15*pi/180)*(sin(lat)*p(t) + h*cos(lat)) lt 2,\
A = -h/tan(lat), B = 0.27, p(t), tan(30*pi/180)*(sin(lat)*p(t) + h*cos(lat)) lt 2, A = -h/tan(lat), B = 0.27, p(t), -tan(30*pi/180)*(sin(lat)*p(t) + h*cos(lat)) lt 2,\
A = -h/tan(lat), B = 0.18, p(t), tan(45*pi/180)*(sin(lat)*p(t) + h*cos(lat)) lt 2, A = -h/tan(lat), B = 0.18, p(t), -tan(45*pi/180)*(sin(lat)*p(t) + h*cos(lat)) lt 2,\
A = -h/tan(lat), B = 0, p(t), tan(60*pi/180)*(sin(lat)*p(t) + h*cos(lat)) lt 2, A = -h/tan(lat), B = 0, p(t), -tan(60*pi/180)*(sin(lat)*p(t) + h*cos(lat)) lt 2,\
A = -h/tan(lat), B = -0.32, p(t), tan(75*pi/180)*(sin(lat)*p(t) + h*cos(lat)) lt 2, A = -h/tan(lat), B = -0.32, p(t), -tan(75*pi/180)*(sin(lat)*p(t) + h*cos(lat)) lt 2,\
A = -h/tan(lat), B = -5, p(t), tan(105*pi/180)*(sin(lat)*p(t) + h*cos(lat)) lt 2, A = -h/tan(lat), B = -5, p(t), -tan(105*pi/180)*(sin(lat)*p(t) + h*cos(lat)) lt 2