Bitirme çalışması yaptırdığım bir öğrencimin projesinde model bir sistem olarak sonlu potansiyel kuyusunu inceliyorduk. Bunun için de nümerik çözümlerden emin olmak lazımdı. İnternette bu işi yaptığını söyleyen birkaç program ve site var onları kullanalım dedik hepsi birbirinden kafa karıştırıcı idi, emin olamadım. Mecburen bu işi yapan bir kodu kendim yazmam gerekti. Ancak olması gerektiğinden çok uzun sürdü bir şekilde bu iş ve nihayet bitti hemen burada yayımlayıp ensemden atmak istiyorum. Açık kod...
Kuantum mekaniğinin standart alıştırmalarından olan bu problemin "çözümü" birçok kaynakta mevcut. Çözümünü tırnak içinde yazdık zira problem analitik olarak çözülemez. Sınır şartlarının eşitlenmesi sonucunda enerji için çıkan ve "ağır şekilde non-lineer" olan bir bilinmeyenli denklem en sade hale getirilip bundan sonra denklemin nümerik olarak çözülmesi gerektiği söylenir.
Bu yazıda denklemin türetilmesini tekrarlayıp nümerik çözüm için bir algoritma vereceğim. Esas nümerik metod üzerinde durmak istediğimden dolayı teori kısmını sadece önemli noktalara değinerek biraz hızlıca geçeceğim. Dediğim gibi birçok kaynaktan detaylara bakılabilir.
Problemi hatırlayalım: -L ile +L koordinatları arasında -V0'a eşit olan ve diğer her yerde 0 olan bir potansiyelde zamandan bağımsız Schrodinger denklemi çözmeye çalışıyoruz. Potansiyeli yukarıda gösterildiği gibi I. bölge, II. bölge ve III. bölge diye işaretleyelim. Kuyunun içerisinde "bağlı" durumlar (bounded states) arıyoruz dolayısı ile enerjimizin -V0 < E < 0 koşullarına uyması gerekir.
I. ve III. bölgedeki çözümün genel hali aşağıdaki gibidir.
Burada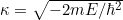 
olurken I. bölgede x < 0 olduğundan ve fonksiyonun normalize edilebilir bir ifade olması şartından dolayı A = 0 olmak zorundadır (aksi takdirde sonsuza patlar). Aynı mantıkla III. bölgedeki çözüm için de B = 0 olmak zorundadır.
II. bölgedeki çözüm ise aşağıdaki şekilde yazılır:
Burada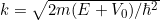 
ifadesi ile verilir. Bundan sonra yapılması gereken -L ve +L deki sınır şartlarında hem fonksiyonları hem de türevlerini eşitlemek ve çıkan denklemlerden E'yi bulmaya çalışmaktır.
Bu noktada işi nispeten kolaylaştıran bir teorem yardımımıza koşar. Eğer potansiyeliniz "çift fonksiyon" ise ( V(x) = V(-x) ise ) o zaman çözümler tek ve çift fonksiyonlar olarak ayrı ayrı incelenebilir. Bu yoldan devam edecek olursak tek çözümler için II. bölgede sadece sinüs çözümünü çift çözümler için ise sadece kosinüs çözümünü alabiliriz.
Çift çözümlerle başlayalım: (üstellerdeki kappa'larla trigonometriklerdeki k'lar karışmasın)
(Çözüm çift olduğu için I. ve III. bölgedeki baş katsayıları eşit aldık.)
Bunların türevlerini de alıp -L ve +L sınırlarındaki eşitlemeleri de yapacak olursak 4 denklem elde ederiz ancak bu denklemler ikişer ikişer birbirleriyle aynı olduklarından sadece aşağıdaki 2'si kalır elde:
Bunları taraf tarafa böldüğümüz zaman:
denklemini elde ederiz. Kappa ile k'nın daha önce verdiğimiz tanımları kullanılarak aralarında bir bağıntı yazmak mümkündür:
Burada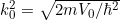 
ifadesinin kısaltmasıdır. Bu bağıntı yardımı ile bir önceki denklemde kappadan kurtulmak ve k cinsinden yazmak mümkündür. Sonuçta denklem aşağıdaki hale gelir:
Korkunç derecede non-lineer olan bu denkleml cepte dursun bir de kardeşini türetelim. (Yani tek çözümlere bakalım) Tek çözümler için yapılması gereken II. bölgede sinüslü çözümü almak ve I. ve III. bölgedeki çözümlerin baş katsayılarının işaretlerinin birini eksili hale getirmektir. Bundan sonra yukarıdaki aşamaların yolundan devam edersek aşağıdaki denklemi elde ederiz.
İki denklemde de sağ taraftaki ifade tanıdıktır: Yarıçapı k0 olan bir çember denklemi. Soldaki ifadeler ise tanjant ve kotanjant fonksiyonunun değişkenin kendisi ile çarpılarak "sivriltilmiş" halidir. Sağ ve sol tarafların çözümlerine aşağıdaki grafik üzerinde bakalım.
Yatay ekseni k olan grafiğimizde dikey eksen denklemlerde sağ ve sol taraflardaki fonksiyonların aldıkları değerleri ifade etmektedir. Siyah ile çizilmiş eğri çeyrek çemberimizden başka birşey değildir. Kırmızı ile çizilen ise çift çözümlerden gelen k.tan(kL) fonksiyonu iken mavi kesikli çizgilerle gösterilen tek çözümlerden gelen -k.cot(kL) fonksiyonudur. İşte mavi ve kırmızı çizgilerin siyah çemberi kestiği noktalara ait olan k değerleri denklemin çözümünü ifade ederler. Bu değerleri bulmak istiyoruz.
Yukarıdaki grafikte inceleme örneği olarak 1 nm genişliğinde 10 eV derinliğinde bir kuyuda bulunan elektron problemi seçilmiştir. Görüldüğü gibi 6 noktada kesişim vardır. Yani bu durumda 6 tane bağlı durum mevcuttur. (Sonlu potansiyelde mümkün olan bağlı durumların sayısı her zaman sonludur.) Grafikten çıkarılabilecek başka güzel yorumlar da vardır. Mesela kuyunun derinliğini arttırırsanız çemberin çapı da artacağından dolayı daha fazla sayıda kesişim noktası (yani bağlı durum enerji seviyesi) olacağı söylenebilir. Yine kuyunun genişliğini arttırmak trigonometrik fonksiyonların "peryotlarını" azaltacağından dolayı çemberin içine daha sık yerleşecekler ve kesişim sayısı artacaktır. Bu güzel grafikte daha fazla kaybolmadan nümerik metodumuza geçelim. Dediğim gibi buraya kadar olanlar ders kitaplarında var. Bundan sonrası ise sadece burada var... :-))
Probleme şöyle yaklaşıyorum: Tanjant ve kotanjant fonksiyonlarının içi pi/2 (ve bazı tek-çift katları) olduğunda sonsuza patlıyor dolayısıyla herşeyden önce bu sonsuzluklardan kaçınmam lazım. Bunun için yatay ekseni pi/2L uzunluğunda dilimlere ayırıyorum ve herbir dilimin içini ayrı ayrı inceliyorum. Birinci, üçüncü, beşinci, vs. tek sayılı dilimlerde çift çözümden gelen denklemi; ikinci dördüncü, vs. çift sayılı dilimlerde de tek çözümden gelen denklemi çözmem lazım.
Tek-çift mantığını bilgisayara anlattıktan sonra her dilimi aradığım hassasiyete göre (genelde binlerce) parçaya bölüyor ve k'nın değerini her parçada hesaplayarak arttırmaya başlıyorum. Trigonometrik değer çemberin değerinden büyük olduğu anda döngüye durmasını söylüyorum ve bu k değerini kaydediyorum. Ondan sonra bir sonraki dilime geçiyorum ve işlemi tekrarlıyorum. Kaç tane dilim kullanacağımı da ilk başta çemberin yarıçapına göre belirliyorum.
Bütün k'lar kaydedildikten ve döngüler tamamlandıktan sonra k'ları basitçe enerji karşılıklarına çeviriyor ve yazdırıyorum. İşte bu işi yapan python dilinde yazılmış bir program:
#################################
from math import pi,tan # Pi sayisi ve tanjant fonksiyonu
h2m = 3.815 # hbar^2 / 2m (eV.Ang^2) birimlerinde m elektron kutlesi
L = 5 # angstrom biriminde DIKKAT !!! KUYU GENISLIGI = 2L dir.
V0 = 10.0 # Kuyunun derinligi eV biriminde
h2m = 3.815 # hbar^2 / 2m (eV.Ang^2) birimlerinde m elektron kutlesi
L = 5 # angstrom biriminde DIKKAT !!! KUYU GENISLIGI = 2L dir.
V0 = 10.0 # Kuyunun derinligi eV biriminde
def cot(x): # math modulunde kotanjant yoktu kendim tanimladim
return 1/tan(x)
def k(n,m): # k'yi bu sekide bir fonksiyon olarak tanimladim.
return (pi*n/(2*L)) + m # n dilim sayisi m ise dilimin icerisindeki adim.
k0_sq = V0/h2m # k0'in karesireturn 1/tan(x)
def k(n,m): # k'yi bu sekide bir fonksiyon olarak tanimladim.
return (pi*n/(2*L)) + m # n dilim sayisi m ise dilimin icerisindeki adim.
k0 = k0_sq**0.5 # k0
adim = 100000 # her bir dilimi yuzbine bolup inceliyorum
m0 = pi/(2*L*float(adim)) # adim arttirma miktari
par_say = int(k0*2*L/pi)+1 #parca sayisi. Bu k0'a gore hesaplaniyor
print par_say,' tane cozum var. Eenrjiler:' # Cozum sayisi ekrana yaziliyor
for n in range(par_say): # Ana dongumuz
m = m0
if n%2 == 0: # Cift cozumler icin
while k(n,m)*tan(k(n,m)*L) < (k0_sq-(k(n,m)**2))**0.5:
m += m0 # adimimizi arttiriyoruz
if k(n,m) > k0: #son parca icin emniyet subabi
break # k nin k0'dan buyuk oldugu anda duruyoruz ve
print h2m*(k(n,m)**2) - V0 # ekrana yaziyoruz.
else: # Tek cozumler, ayni mantik
while -1*k(n,m)*cot(k(n,m)*L) < (k0_sq - (k(n,m)**2))**0.5:
m += m0
if k(n,m) > k0:
break
print h2m*(k(n,m)**2) - V0 # Bazi kitaplar kuyunun dibini 0 alir o zaman V0'i
# silebilirsiniz.
######################################
Yukarıdaki grafikte verilen örnek için yazılmış bu kodu çalıştırdığımızda enerji değerleri eV cinsinden aşağıdaki gibi bulunur:
6 tane cozum var. Enerjiler:-9.70204904621
-8.81234584649
-7.34506318636
-5.33167725429
-2.8477862078
-0.223618800482
Hiç yorum yok:
Yorum Gönder